suivant: Force monter: Modélisation de l'effort sur précédent: Changement de base de

Correctif apporté à  la modélisation de l'effort

Nous n'avons pas pris en compte la composante suivant 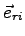$\vec e_{ri}$ de la vitesse de l'air par rapport à  la pale $i$. Gérons ici cette vitesse.

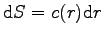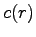La force élémentaire exercée sur une surface élémentaire d'aire  $\mbox{d}S=c(r) \mbox{d}r$ de la pale $i$, de largeur $c(r)$, est modélisée par :

 $$\left.\begin{array}{l} \mbox{d}\vec F_i = - \mbox{d}T_i \vec... ...x \> \mbox{d}S \\ [3mm] f = \frac{C_z}{C_x} \end{array}\right.$$

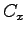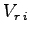où les coefficients aérodynamiques $C_x$ et $C_z$ ne sont pas forcément identiques àceux des chapitres précédents et où la vitesse $V_{r\>i}$ est différente pour chaque pale $i$ :

 $$V_{r\>i} = (\Omega r \vec e_{\theta\>i} - V \vec x)\cdot\vec e_{r\>i} = - V \vec x\cdot\vec e_{r\>i}$$

où

 $$\begin{eqnarray*} \vec x\cdot\vec e_{r\>1} &=& \cos\psi \\ \vec x\cdot\vec e_{r... ...psi ) \\ V_{r\>3} &=& \frac V 2 ( \cos\psi - \sqrt 3 \sin\psi) \end{eqnarray*}$$

Cette vitesse 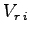$V_{r\>i}$ sur la pale $i$ évolue sur 1 tour et n'est pas toujours positive.

• Lorsque 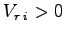$V_{r\>i}>0$, c'est le bout de pale qui voit arriver l'air et l'effort engendré doit être notable ;
• Par contre lorsque 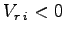$V_{r\>i}<0$, c'est le centre du boom (ou plutôt les autres pales !) qui voit arriver l'air.

De ce fait on ne considèrera _ par la suite _ de force due à cette vitesse que lorsque 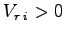$V_{r\>i}>0$ soit : V_r1>0     [ pi/2 ; 3.pi/2 ]   ;   V_r2>0     [ - pi/6 ; 5.pi/6 ]   ;    V_r3>0     [ -5.pi/6 ; pi/6 ]

 Sous-sections

• Force
• Moment en $O$
• Conclusion
• Critique

suivant: Force monter: Modélisation de l'effort sur précédent: Changement de base de