-
![$\psi \in \left[ -\frac{\pi} 6 ; \frac{\pi} 6 \right]$](img203.png) seul
seul
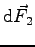 et
et
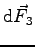 existent ;
existent ;
-
![$\psi \in \left[ \frac{\pi} 6 ; \frac{3\pi} 6 \right]$](img206.png) seul
seul
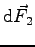 existe ;
existe ;
-
![$\psi \in \left[ \frac{3\pi} 6 ; \frac{5\pi} 6 \right]$](img207.png) seul
seul
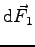 et
et
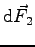 existent ;
existent ;
Il faut alors faire la somme des forces élémentaires sur tout le boomerang en sachant que :
|
|
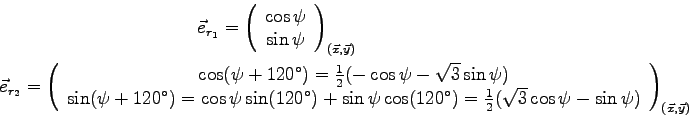
soit pour la force élémentaire sur ces 2 pales :
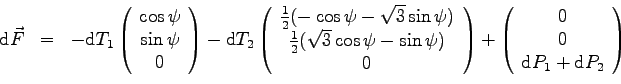

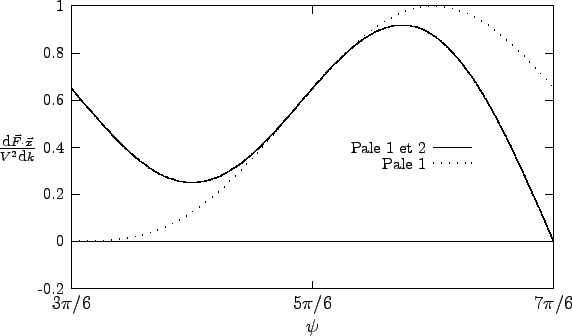 |
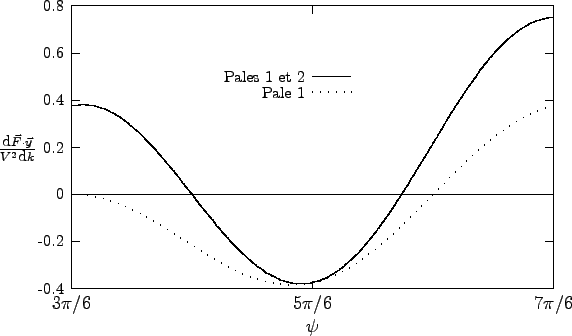
Sur ce graphe, il faut voir la courbe sur les pales 1 et 2 pour puis la courbe sur la pale 1 pour on remarque la continuité des 2 courbes en |
Donc pour
![]() :
:
![]()
et pour
![]() :
:
![]()
On déduit du tracé que :
![]()
puis :
![]()
où ![]() est toujours la surface d'une pale.
est toujours la surface d'une pale.
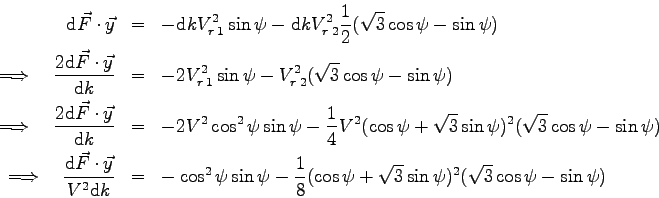
 |
Sur ce graphe, il faut voir la courbe sur les pales 1 et 2 pour la courbe sur la pale 1 pour on remarque la continuité des 2 courbes en |
Donc pour
![]() :
:
![]()
et pour
![]()
![]()
On déduit du tracé que :
La composante de
![]() sur
sur ![]() est pour
est pour
![]() :
:
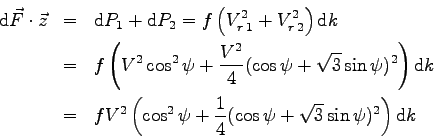
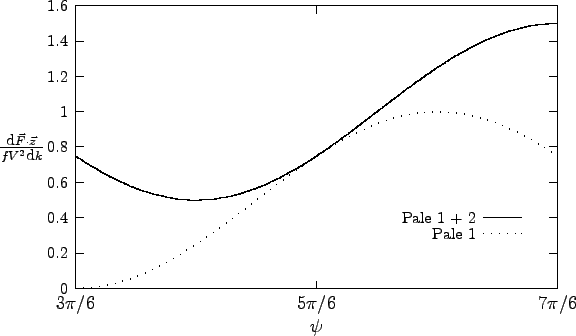 |
Evolution de la force suivant sur ce graphe, il faut voir la courbe sur les pales 1 et 2 pour la courbe sur la pale 1 pour on remarque la continuité des 2 courbes en |