suivant: Remarques monter: Analyse des efforts sur précédent: Comparaison poids et portance

Effort sur ces profils après une demi révolution

Par curiosité, on peut calculer les efforts sur ces mêmes profils après une demi révolution du tripale, les vitesses de rotation et de translation se soustrayant alors.

Le 1^er profil situé à $r_1=130$ mm de l'axe de rotation propre avance dans un air immobile à la vitesse  $V'_1=-V+\Omega r_1=3.75$ m/s.
Le nombre de Reynolds relatif à l'écoulement est  ${\cal R}'_1 = \frac{V'_1 c_1}{\nu} = 9509$.
De la même manière que précédement, on obtient les coefficients aérodynamiques au nombre de Reynolds qui nous intéresse :

${\cal R}$	8000	9509	12000
$C_z$	0.1065	0.0887	0.0594
$C_x$	0.0527	0.0498	0.0449

On remarque ici une grande variation de $C_z$ entre ${\cal R}=8000$ et $12000$. La valeur estimée à ${\cal R}=9509$, à savoir $0.0887$, est donc approchée et très certainement fausse. Il faudrait refaire des calculs avec Xfoil.
Nous pouvons alors déterminer les forces qui s'exercent sur $\mbox{d}e=1$ mm de longueur de pale :

 $$\displaylines{ \mbox{la force de trainée : } \mbox{d}T_1' = ... ..._z V_1^2 = 0.029 \mbox{ mN} \approx \frac 1 {472} \mbox{d}P_1 }$$

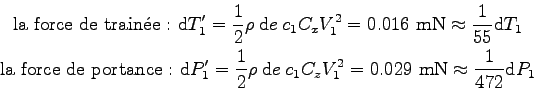
On se rend compte que de ce côté, le profil ne porte quasiment plus alors qu'il pèse tout autant ! Les forces de trainée sont plus faibles mais ne diminuent pas autant que celles de portance !

Si l'on refait ces calculs pour le 2^nd profil situé à $r_2=95$ mm, on s'aperçoit que  $\Omega r_2 < V$ ce qu'il fait que c'est le bord de fuite qui attaque l'air immobile ! ...pour ces valeurs imposées de façon arbitraire de $\Omega$ et $V$.

suivant: Remarques monter: Analyse des efforts sur précédent: Comparaison poids et portance