suivant: Forces sur le 2nd profil monter: Analyse des efforts sur précédent: Analyse des efforts sur

Forces sur le 1^er profil

Le 1^er  profil, "manu4_38" (4 mm d'épaisseur pour 38 mm de largeur), est situé à $r_1=130$ mm de l'axe de rotation propre. La vitesse de rotation $\Omega$ engendre une vitesse linéaire  $\Omega r_1=20.42$ m/s.
La vitesse de translation se cumule quasiment à cette vitesse précédent [en réalité pas exactement pour la position du tripale de la FIG. 1 : $V$, $\Omega r_1$ et $\Omega r_2$ ont 3 directions légèrement différentes]. On peut donc supposer que le profil avance dans un air immobile à la vitesse  $V_1=V+\Omega r_1=37.09$ m/s.
Ce profil possède une largeur $c_1=38$ mm.
Le nombre de Reynolds relatif à l'écoulement est  ${\cal R}_1 = \frac{V_1 c_1}{\nu} = 93954$ où la viscosité cinématique de l'air est  $\nu=0.15\>10^{-4}$ m$^2$.s$^{-1}$[Ceci est une valeur standard. Il faut cependant savoir que la viscosité de l'air dépend de sa température et de sa pression.].

Des calculs [réalisés avec le logiciel gratuit Xfoil http://raphael.mit.edu/xfoil/index.html] aérodynamiques sur ce profil [http://perso.univ-rennes1.fr/laurent.blanchard/Profils/manu4_38/index.html] permettent de déterminer les coefficients aérodynamiques à différents nombres de Reynolds et d'obtenir (par interpolation linéaire) la valeur de ces coefficients aérodynamiques au nombre de Reynolds qui nous intéresse

${\cal R}$	90000	93954	100000
$C_z$	0.4332	0.4229	0.4072
$C_x$	0.02790	0.02752	0.02694

cf §8

Nous pouvons alors déterminer les forces aérodynamiques qu'exerce l'air (de masse volumique $\rho=1.24$ kg.m$^{-3}$) sur $\mbox{d}e=1$ mm de longueur de pale :

 $$\displaylines{ \mbox{la force de trainée : } \mbox{d}T_1 = \... ...rac 1 2 \rho \> \mbox{d}e \> c_1 C_z V_1^2 = 13.70 \mbox{ mN} }$$

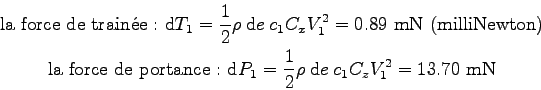
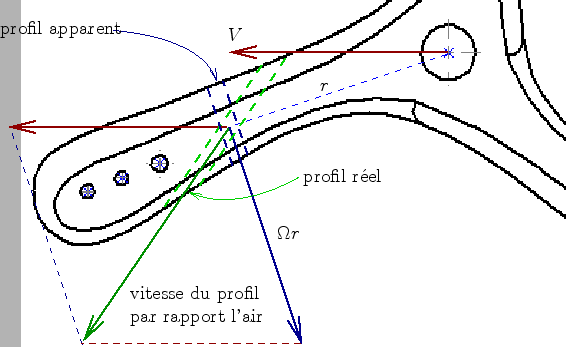
On pourrait effectuer ces calculs pour différents profils du tripale bien que l'on va se confronter au problème entre profil apparent et profil réel (dans le précédent calcul, pour obtenir $V_1$, on a additionné bêtement les vitesses $V$ et $\Omega r_1$ alors que pour la plupart des profils ces 2 vitesses n'ont pas la même direction).

suivant: Forces sur le 2nd profil monter: Analyse des efforts sur précédent: Analyse des efforts sur