suivant: Section et moment quadratique
monter: Résumé
précédent: Comparaison avec le modèle
On ne peut chercher le centre de poussée que s'il existe c-à-d que si
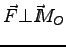 . On ne va donc considérer que certaines composantes à savoir :
. On ne va donc considérer que certaines composantes à savoir : 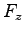 ,
,
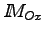 et
et
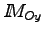 .
.
Déterminons la position du centre de poussée  situé dans le plan du tripale au même niveau que
situé dans le plan du tripale au même niveau que  :
:
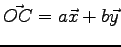 qui est caractérisé par :
qui est caractérisé par :
Vu que
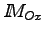 ,
,
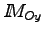 sont fonction de
sont fonction de  (
(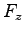 n'est pas fonction de
n'est pas fonction de  ), la position du centre de poussée va évoluer en fonction de
), la position du centre de poussée va évoluer en fonction de  :
: 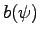 et
et 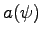 .
.
Jérome Royo (Champion de France 2007) a eu l'idée (cf magasine Profil n 21) de
connaître la position du centre de poussée lors d'un tour
du boomerang. On peut alors connaître avec ce qui
précède la position de
21) de
connaître la position du centre de poussée lors d'un tour
du boomerang. On peut alors connaître avec ce qui
précède la position de  sur 1 tour (ou plutôt sur 1/3 de tour) mais on s'aperçoit qu'elle dépend des valeurs de
sur 1 tour (ou plutôt sur 1/3 de tour) mais on s'aperçoit qu'elle dépend des valeurs de 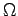 et
et 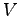 pour un tripale donné !
pour un tripale donné !
![\begin{figure}\begin{center}\setlength{\unitlength}{0.240900pt}
\ifx\plotpoin...
....200pt]{0.400pt}{0.723pt}}
\end{picture}\input{cp2.gnu}
\end{center}\end{figure}](img103.png) |
Evolution de la position du centre de poussée sur un tiers de tour d'un tripale ...
( défini par largeur de pale 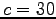 mm, rayon maxi mm, rayon maxi  mm et mini mm et mini 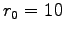 mm ) mm )
... pour une vitesse linéaire  m.s m.s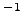
et pour 2 vitesses de rotation différentes
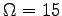 tr/s (en haut tr/s (en haut 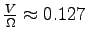 m) m)
et
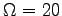 tr/s (en bas tr/s (en bas
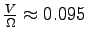 m) m) |
En considérant les valeurs moyennes des efforts, la position moyenne du centre de poussée est donnée par :
Pour une pale rectangulaire où 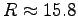 cm et
cm et 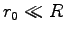 on a :
on a :
On peut alors examiner la position moyenne du centre de poussée est fonction du rapport
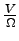 exprimé en m.
Le maximum de cette courbe situé pour
exprimé en m.
Le maximum de cette courbe situé pour
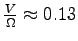 m laisse prétendre qu'il existe une valeur optimum de ce rapport
qui donnera un centre de poussée le plus éloigné
possible (
m laisse prétendre qu'il existe une valeur optimum de ce rapport
qui donnera un centre de poussée le plus éloigné
possible (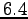 cm soit 4/10ème de
cm soit 4/10ème de 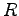 ) du centre de gravité
) du centre de gravité  donc un effet gyroscopique plus important bien qu'il faille faire
attention à ce genre de phrase ! La comparaison doit être
faite avec des termes constants !
donc un effet gyroscopique plus important bien qu'il faille faire
attention à ce genre de phrase ! La comparaison doit être
faite avec des termes constants !
Pour avoir une idée :
- si
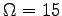 tr/s alors ce maximum est pour
tr/s alors ce maximum est pour 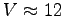 m/s
m/s 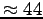 km.h
km.h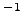 . A cette vitesse linéaire, un tripale d'une portée de 20 m (
. A cette vitesse linéaire, un tripale d'une portée de 20 m (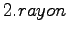 ) parcours environ 62 m (
) parcours environ 62 m (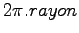 ) en un temps de 5.1 s soit 58 vols lors d'un round d'endurance de 5mn, sans compter les temps de transition !
) en un temps de 5.1 s soit 58 vols lors d'un round d'endurance de 5mn, sans compter les temps de transition !
- si
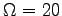 tr/s alors ce maximum est pour
tr/s alors ce maximum est pour 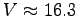 m/s
m/s 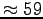 km.h
km.h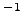 . A cette vitesse linéaire, un tripale d'une portée de 20 m (
. A cette vitesse linéaire, un tripale d'une portée de 20 m (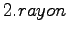 ) parcours environ 62 m (
) parcours environ 62 m (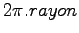 ) en un temps de 3.85 s soit 78 vols lors d'un round d'endurance de 5mn, sans compter les temps de transition !
) en un temps de 3.85 s soit 78 vols lors d'un round d'endurance de 5mn, sans compter les temps de transition !
suivant: Section et moment quadratique
monter: Résumé
précédent: Comparaison avec le modèle
Laurent Blanchard
2007-12-29
![]() . On ne va donc considérer que certaines composantes à savoir :
. On ne va donc considérer que certaines composantes à savoir : ![]() ,
,
![]() et
et
![]() .
.
![]() situé dans le plan du tripale au même niveau que
situé dans le plan du tripale au même niveau que ![]() :
:
![]() qui est caractérisé par :
qui est caractérisé par :
![\begin{displaymath}\displaylines{
\vec I \kern-4.5pt M(C) = \vec 0 \quad\Longrig...
...[ 4 \frac {\Omega^2}{V^2} I + 2 S \right]}
\end{array}\right.
}\end{displaymath}](img92.png)
![]() ,
,
![]() sont fonction de
sont fonction de ![]() (
(![]() n'est pas fonction de
n'est pas fonction de ![]() ), la position du centre de poussée va évoluer en fonction de
), la position du centre de poussée va évoluer en fonction de ![]() :
: ![]() et
et ![]() .
.
![]() 21) de
connaître la position du centre de poussée lors d'un tour
du boomerang. On peut alors connaître avec ce qui
précède la position de
21) de
connaître la position du centre de poussée lors d'un tour
du boomerang. On peut alors connaître avec ce qui
précède la position de ![]() sur 1 tour (ou plutôt sur 1/3 de tour) mais on s'aperçoit qu'elle dépend des valeurs de
sur 1 tour (ou plutôt sur 1/3 de tour) mais on s'aperçoit qu'elle dépend des valeurs de ![]() et
et ![]() pour un tripale donné !
pour un tripale donné !
![\begin{figure}\begin{center}\setlength{\unitlength}{0.240900pt}
\ifx\plotpoin...
....200pt]{0.400pt}{0.723pt}}
\end{picture}\input{cp2.gnu}
\end{center}\end{figure}](img103.png)
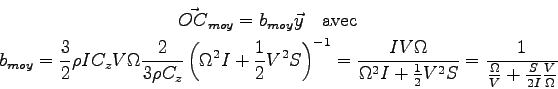
![\begin{picture}(1500,900)(0,0)
\font\gnuplot=cmr10 at 10pt
\gnuplot\sbox{\plot...
...t}{0.400pt}}
\put(1424.0,175.0){\rule[-0.200pt]{3.613pt}{0.400pt}}
\end{picture}](img109.png)