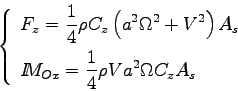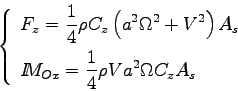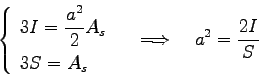suivant: centre de poussée monter: Résumé précédent: Résumé

Comparaison avec le modèle de Dr Hugh Hunt (University of Cambridge)

Dr Hugh Hunt donne :

 $$\left\{\begin{array}{l} \displaystyle F_z = \frac 1 4 \rho C... ..._{Ox} = \frac 1 4 \rho V a^2 \Omega C_z A_s \end{array}\right.$$

En comparant ces équations et les miennes, il vient :

 $$\left\{\begin{array}{l} \displaystyle 3I = \frac {a^2} 2 A_s... ...\end{array}\right. \quad\Longrightarrow\quad a^2 = \frac{2I} S$$

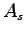$A_s$ est alors la surface du tripale alors que le British annonce que c'est la surface balayée 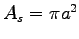$A_s=\pi a^2$ ?! ce qui définit une seconde fois $a$ ?!
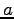On retrouvera le terme 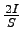$\frac{2I} S$ dans les calculs suivants.