suivant: Résumé
monter: Tripale
précédent: Force
Le moment en  de la force
de la force
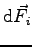 possède une composante sur
possède une composante sur 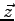 qui provient de
qui provient de 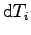 et des composantes suivant
et des composantes suivant 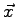 et
et 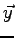 qui proviennent de
qui proviennent de 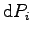 :
:
et le moment en  de la force élémentaire exercée sur l'ensemble des
surfaces élémentaires analogues des 3 pales.
de la force élémentaire exercée sur l'ensemble des
surfaces élémentaires analogues des 3 pales.
Effectuons les 2 sommes une à une :
la seconde :
ce qui nous donne :
puis la première :
Calculons chacune des composantes de ce vecteur :
Cette composante de moment élémentaire varie autour d'une valeur moyenne :
Cette composante de moment
élémentaire varie autour d'une valeur moyenne nulle du
fait de l'hypothèse sur la position du centre de poussée
sur le profil (
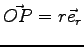 )
: c'est cette composante de moment qui a tendance à faire
monter ou descendre le tripale suivant la position de ce centre de
poussée sur le profil.
)
: c'est cette composante de moment qui a tendance à faire
monter ou descendre le tripale suivant la position de ce centre de
poussée sur le profil.
En considérant les valeurs moyennes de
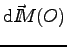 , on peut évaluer (la valeur moyenne) du moment en
, on peut évaluer (la valeur moyenne) du moment en  de l'action de l'air sur l'ensemble du tripale :
de l'action de l'air sur l'ensemble du tripale :
On remarque à nouveau l'expression des moments "quintique" 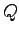 , quadratique
, quadratique  et statique
et statique 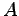 d'une pale
d'une pale  .
.
suivant: Résumé
monter: Tripale
précédent: Force
Laurent Blanchard
2007-12-29
![]() de la force
de la force
![]() possède une composante sur
possède une composante sur ![]() qui provient de
qui provient de ![]() et des composantes suivant
et des composantes suivant ![]() et
et ![]() qui proviennent de
qui proviennent de ![]() :
:
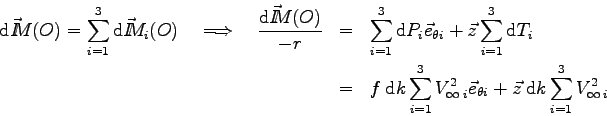
![\begin{eqnarray*}
\sum_{i=1}^3 V_{\infty\>i}^2 &=&
(\Omega r + V \sin\psi)^2
...
...^2\psi + \sin^2\psi) ]
\\
&=& [3\Omega^2 r^2 + \frac {3V^2} 2 ]
\end{eqnarray*}](img65.png)
![\begin{displaymath}
\mbox{d}\vec I \kern-4.5pt M(O) \cdot \vec z = -[3\Omega^2 r...
...x \left[ 3\Omega^2 r^2 + \frac {3V^2} 2 \right] r \> \mbox{d}S
\end{displaymath}](img66.png)
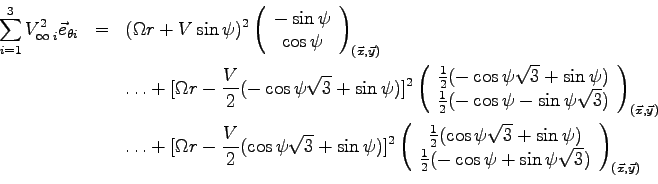
![\begin{eqnarray*}
\frac{\mbox{d}\vec I \kern-4.5pt M(O)\cdot\vec x}{-rf\>\mbox{d...
...mega r} V \right]}_{f(\psi,\frac{\Omega r} V)} r \>\mbox{d}k
\\
\end{eqnarray*}](img68.png)
![\begin{picture}(1500,900)(0,0)
\font\gnuplot=cmr10 at 10pt
\gnuplot\sbox{\plot...
...t}{0.562pt}}
\put(1106.0,315.0){\rule[-0.400pt]{3.132pt}{0.800pt}}
\end{picture}](img69.png)
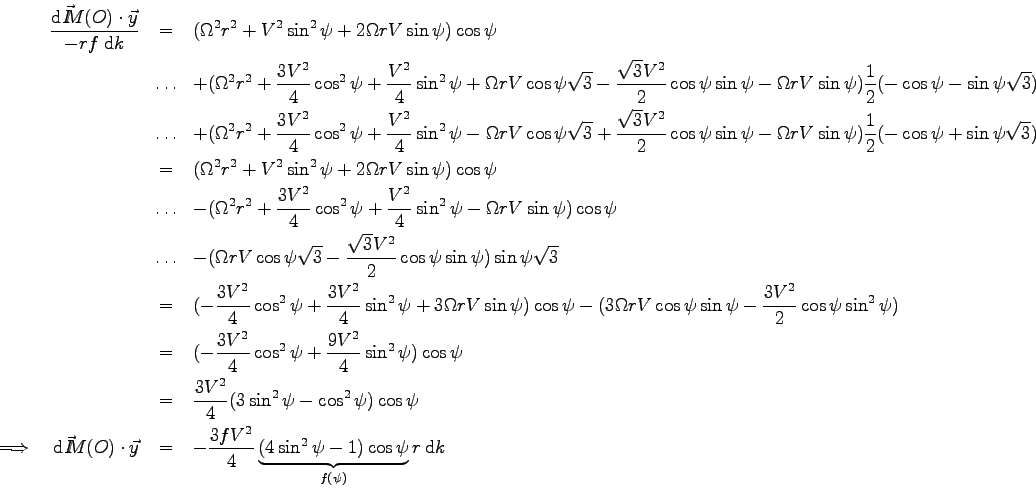
![\begin{picture}(1500,900)(0,0)
\font\gnuplot=cmr10 at 10pt
\gnuplot\sbox{\plot...
...t}{0.400pt}}
\put(1216.0,794.0){\rule[-0.200pt]{3.132pt}{0.400pt}}
\end{picture}](img72.png)
![]() , on peut évaluer (la valeur moyenne) du moment en
, on peut évaluer (la valeur moyenne) du moment en ![]() de l'action de l'air sur l'ensemble du tripale :
de l'action de l'air sur l'ensemble du tripale :
![\begin{eqnarray*}
\vec I \kern-4.5pt M(O) &=& \int_{r_0}^R \mbox{d}\vec I \kern-...
...3 2 \rho C_x \left[ \Omega^2 Q + \frac {V^2} 2 A \right] \vec z
\end{eqnarray*}](img74.png)