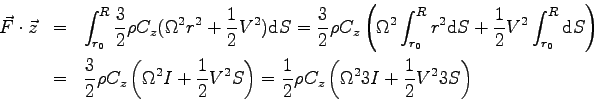suivant: Moment en
monter: Tripale
précédent: Modélisation de l'action air-boomerang
Il faut alors faire la somme des forces élémentaires sur tout le boomerang.
Pour effectuer cette somme regroupons les forces élémentaires exercées sur chacune des 3 pales :
projettons dans la base
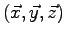 :
:
soit pour la force élémentaire sur les 3 pales :
La composante de
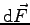 sur
sur 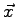 est :
est :
Le premier terme de cette composante de force varie autour d'une valeur
moyenne nulle alors que le second est constant quelque soit l'angle  .
.
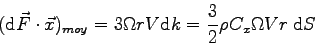
Cette composante de force a tendance (entre autres) à freiner la translation du boomerang.
La composante de
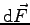 sur
sur 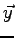 est :
est :
Cette composante de force varie autour d'une valeur moyenne nulle.
La composante de
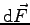 sur
sur 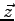 est :
est :
On remarque essentiellement que cette composante de force élémentaire ne dépend pas de  !
!
Cette composante de force est à l'origine de l'effet gyroscopique.
Nous avons obtenu la force élémentaire moyenne (sur 1
tour) exercée sur l'ensemble des surfaces
élémentaires analogues des 3 pales.
Pour obtenir la force globale sur le tripale, il suffit
d'intégrer chacune des composantes :
où  ,
, 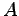 , et
, et  désignent respectivement les moments quadratique et statique et la section d'une pale et
désignent respectivement les moments quadratique et statique et la section d'une pale et 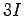 ,
, 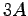 et
et 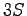 les moments quadratique et statique et la section du tripale.
les moments quadratique et statique et la section du tripale.
Rem : On retrouve cette notion de moments quadratique et statique "Résistance des Matériaux".
suivant: Moment en
monter: Tripale
précédent: Modélisation de l'action air-boomerang
Laurent Blanchard
2007-12-29
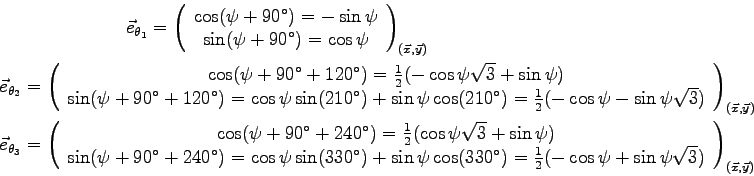
![\begin{eqnarray*}
\mbox{d}\vec F &=&
- \mbox{d}T_1 \left(\begin{array}{c}
-\sin\...
...rac V 2 (\cos\psi\sqrt 3 + \sin\psi))^2 ]
\end{array}\right)
\\
\end{eqnarray*}](img44.png)
![\begin{eqnarray*}
\frac{\mbox{d}\vec F \cdot \vec x}{\mbox{d}k} &=&
(\Omega r ...
...^2\psi - 9\cos^2\psi) \sin\psi + 6 \Omega r V \right] \mbox{d}k
\end{eqnarray*}](img47.png)
![]() sur
sur ![]() est :
est :
![\begin{eqnarray*}
\frac{\mbox{d}\vec F \cdot \vec y}{\mbox{d}k} &=&
-(\Omega r ...
...os^2\psi -9 \sin^2\psi ) -6\Omega r V \sin\psi \right] \mbox{d}k
\end{eqnarray*}](img50.png)
![]() sur
sur ![]() est :
est :
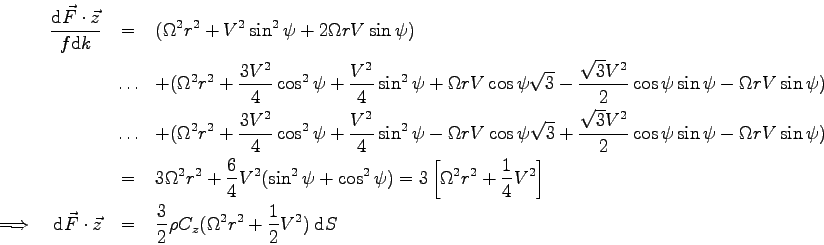
![]() !
!