Modélisation de l'action air-boomerang

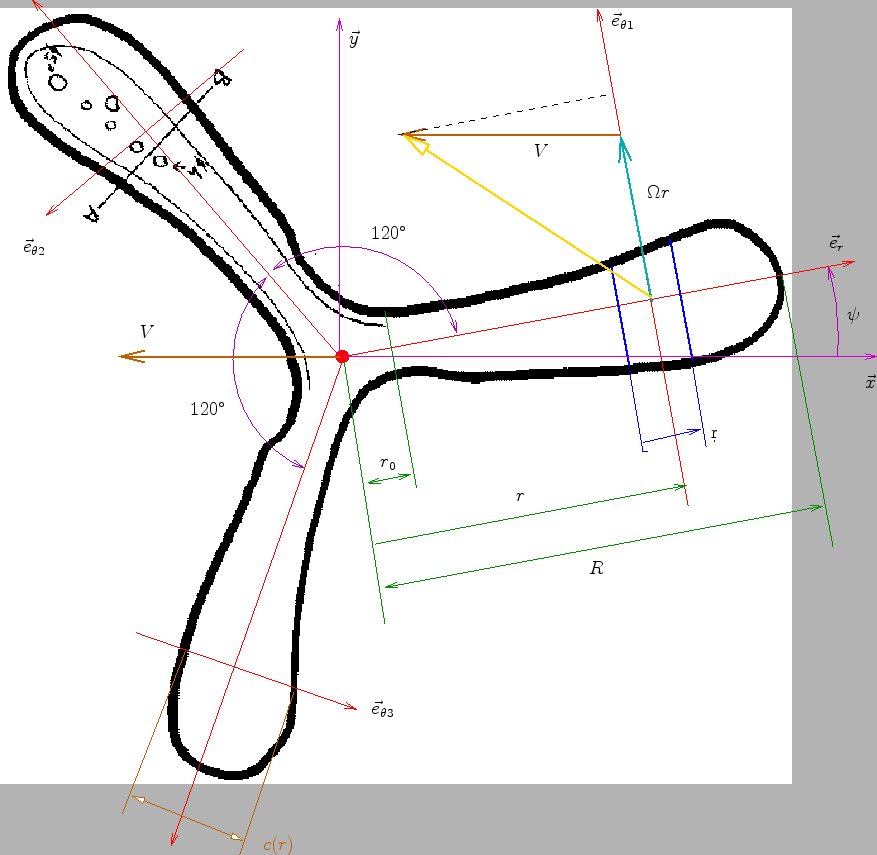
La force élémentaire exercée sur une surface élémentaire d'aire $\mbox{d}S=c(r) \mbox{d}r$ de la pale

, de largeur

, est modélisée par :

$\begin{displaymath} \left.\begin{array}{l} \mbox{d}\vec F_i = - \mbox{d}T_i \vec... ...x \> \mbox{d}S \\ [3mm] f = \frac{C_z}{C_x} \end{array}\right. \end{displaymath}$

$\begin{displaymath} V_{\infty\>i} = (\Omega r \vec e_{\theta\>i} - V \vec x)\cdot\vec e_{\theta\>i} = \Omega r - V \vec x\cdot\vec e_{\theta\>i} \end{displaymath}$

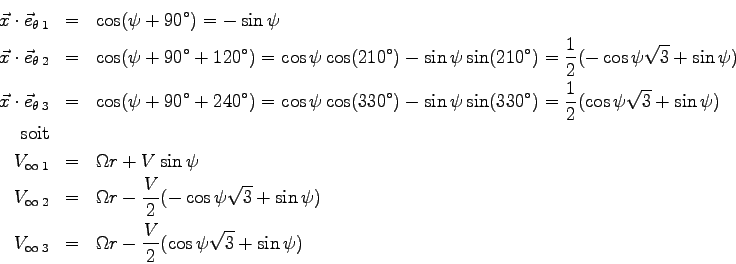
$\begin{eqnarray*} \vec x\cdot\vec e_{\theta\>1} &=& \cos(\psi+90^\circ) = -\sin\... ...infty\>3} &=& \Omega r - \frac V 2 (\cos\psi\sqrt 3 + \sin\psi) \end{eqnarray*}$

Evolution de la vitesse de l'air par rapport à la pale sur un tour de celle-ci et cela pour chacune des 3 pales mais aussi pour cm, $\Omega=20$ tr.s $^{-1}$ et m.s $^{-1}$
$\begin{figure}\begin{center}\setlength{\unitlength}{0.240900pt} \ifx\plotpoin... ...723.0){\rule[-0.400pt]{3.132pt}{0.800pt}} \end{picture} \end{center}\end{figure}$

On remarque alors que $V_{\infty\>i}$ peut être négatif : cela signifie que ce n'est plus le bord d'attaque qui attaque l'air mais le bord de fuite !

Le modèle précédent est alors incorrect car il ne gère pas ce phénomène. En effet pour les profils où $V_{\infty\>i}<0$ , il faudrait écrire :

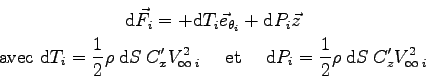
$\begin{displaymath}\displaylines{ \mbox{d}\vec F_i = + \mbox{d}T_i \vec e_{\thet... ...{d}P_i = \frac 1 2 \rho \> \mbox{d}S \> C_z' V_{\infty\>i}^2 }\end{displaymath}$

Lors de la rotation de la pale 1, il y aura une valeur de

à partir de laquelle $V_{\infty\>i}$ sera négatif sur une certaine plage de $\psi$ comprise entre $] \pi ; 2 \pi[$ bien que cela dépende des valeurs de $\Omega$ et


$\begin{figure}\begin{center}\setlength{\unitlength}{0.240900pt} \ifx\plotpoin... ...397.0){\rule[-0.400pt]{6.263pt}{0.800pt}} \end{picture} \end{center}\end{figure}$	Evolution de la vitesse de l'air par rapport à une pale sur un tour de celle-ci pour différents rayons et pour $\Omega=20$ tr.s $^{-1}$ et m.s $^{-1}$ : c'est à partir de r~12 cm que $V_{\infty\>i}<0$ pour une certaine plage de $\psi$ autour de 3pi/2. Evolution de la vitesse de l'air par rapport à une pale sur un tour de celle-ci pour différents rayons et pour $\Omega=10$ tr.s $^{-1}$ et m.s $^{-1}$ : c'est à partir de r~9.5 cm que $V_{\infty\>i}<0$ pour une certaine plage de $\psi$ autour de 3pi/2.