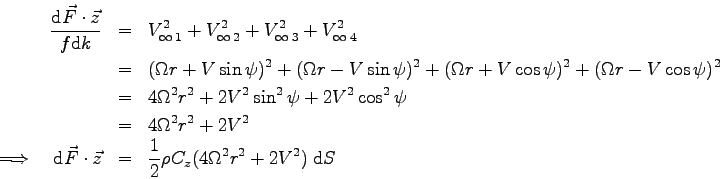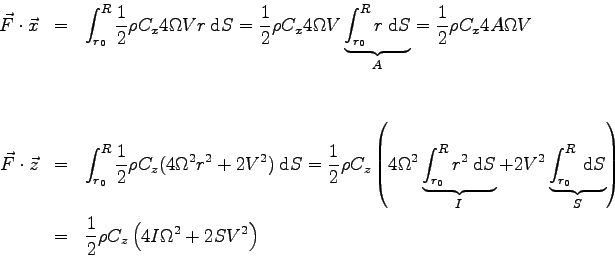suivant: Moment en
monter: Quadripale
précédent: Modélisation de l'action air-boomerang
Il faut alors faire la somme des forces élémentaires sur tout le boomerang.
Pour effectuer cette somme regroupons les forces élémentaires exercées sur chacune des 3 pales :
projettons dans la base
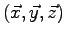 :
:
soit pour la force élémentaire sur les 4 pales :
La composante de
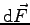 sur
sur 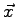 est calculée par :
est calculée par :
On remarque essentiellement que cette composante de force est constante sur un tour (ne dépend pas de  ).
).
La composante de
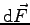 sur
sur 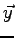 est calculée par :
est calculée par :
On remarque essentiellement que cette composante de force est nulle.
La composante de
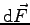 sur
sur 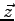 est calculée par :
est calculée par :
On remarque essentiellement que cette composante de force élémentaire ne dépend pas de  !
!
Nous avons obtenu la force
élémentaire exercée sur l'ensemble des surfaces
élémentaires analogues des 4 pales.
Pour obtenir la force globale sur le quadripale il suffit
d'intégrer chacune des composantes :
où  ,
, 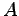 , et
, et  désignent respectivement les moments quadratique et statique et la section d'une pale et
désignent respectivement les moments quadratique et statique et la section d'une pale et 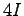 ,
, 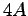 et
et 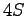 les moments quadratique et statique et la section du quadripale.
les moments quadratique et statique et la section du quadripale.
On retrouve exactement les mêmes types d'expressions "moyennes" que pour un tripale.
suivant: Moment en
monter: Quadripale
précédent: Modélisation de l'action air-boomerang
Laurent Blanchard
2007-12-29
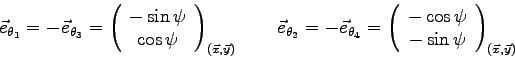
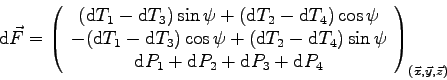

![]() sur
sur ![]() est calculée par :
est calculée par :
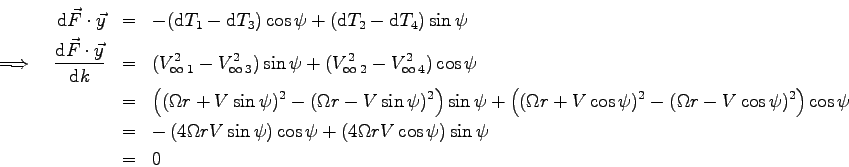
![]() sur
sur ![]() est calculée par :
est calculée par :