suivant: Exploitation monter: Analyse des efforts sur précédent: Remarques

Evolution des efforts sur 1 pale

Analysons, de la même manière que précédemment, les variations des efforts sur une pale lorsqu'elle est en position verticale haute pour les mêmes vitesses de rotation $\Omega$ et linéaire $V$ que précédemment

$V=60$ km/h         $\Omega=25$ tr/s
$r$	$c$	$V+\Omega r$	${\cal R}$	$C_x$	$C_z$	$$\frac{\mbox{d}T}{\mbox{d}e}$$	$$\frac{\mbox{d}P}{\mbox{d}e}$$
(mm)	(mm)	(m/s)				($10^{-3}$ N/mm)	($10^{-3}$ N/mm)
40	28	22.95	42840	0.05042	0.5059	0.4611	4.6256
52	25	24.83	41391	0.05738	0.5281	0.5485	5.0490
72	25	27.98	46627	0.07565	0.6090	0.6881	6.5151
78	26	28.92	50126	0.05353	0.5372	0.7216	7.2424
88	28	30.49	56914	0.04619	0.5156	0.7454	8.3218
98	30	32.06	64121	0.04109	0.4966	0.7856	9.4943
108	33	33.63	73989	0.03450	0.4719	0.7983	10.9204
116	35	34.89	81405	0.03124	0.4552	0.8250	12.0217
120	36	35.52	85239	0.02986	0.4492	0.8408	12.6482
130	38	37.09	93954	0.02907	0.4416	0.8860	13.7786
138	38	38.34	97137	0.02700	0.4201	0.9354	14.5550

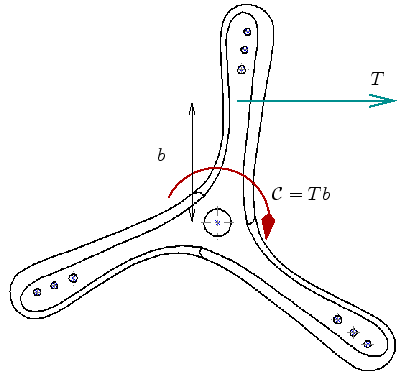
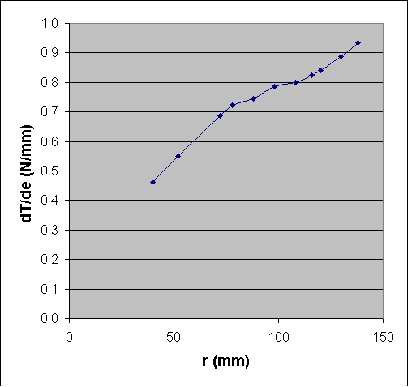
On peut tracer l'évolution de la force (répartie _ exprimée en Newton par millimètre de longueur de pale) de trainée le long de la pale (en fonction de 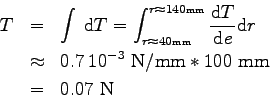$r$). La force de trainée globale sur cette pale sera calculée par :  $$\begin{eqnarray*} T &=& \int \> \mbox{d}T = \int_{r \approx 40 \mbox{\tiny mm}}^... ... \> 10^{-3} \mbox{ N/mm} * 100 \mbox{ mm} \\ &=& 0.07 \mbox{ N} \end{eqnarray*}$$ Cette intégrale est représentée par l'aire sous la courbe.

De même, on trace l'évolution de la force (répartie _ exprimée en Newton par millimètre de longueur de pale) de portance le long de la pale. La force de portance globale sur cette pale sera calculée par :  $$\begin{eqnarray*} P &=& \int \> \mbox{d}P = \int_{r \approx 40 \mbox{\tiny mm}}^... ... \> 10^{-3} \mbox{ N/mm} * 100 \mbox{ mm} \\ &=& 0.9 \mbox{ N} \end{eqnarray*}$$ Cette intégrale est représentée par l'aire sous la courbe.

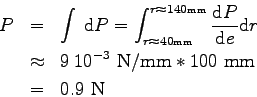
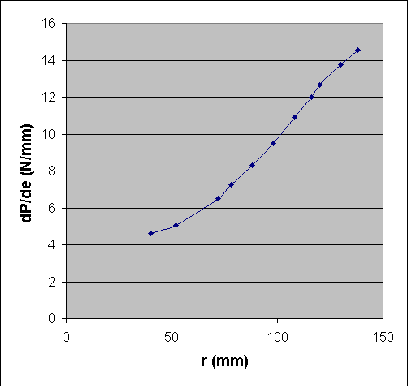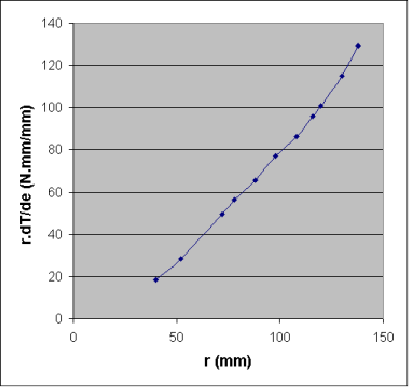
De même, on trace l'évolution du couple (réparti _ exprimé en Newton.millimètre par millimètre de longueur de pale) de freinage engendré par la trainée le long de la pale. Le couple de freinage global sur cette pale sera calculée par : 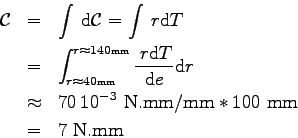 $$\begin{eqnarray*} {\cal C} &=& \int \> \mbox{d}{\cal C} = \int \> r \mbox{d}T \... ...10^{-3} \mbox{ N.mm/mm} * 100 \mbox{ mm} \\ &=& 7 \mbox{ N.mm} \end{eqnarray*}$$ Cette intégrale est représentée par l'aire sous la courbe.

Ce couple  ${\cal C} = 7 \mbox{ N.mm}$ provient de la trainée  $T = 0.07 \mbox{ N}$, on peut en déduire une distance $b$ telle que  ${\cal C} = T b$ qui vaut $b=100$ mm. C'est comme si la force globale de trainée s'appliquait à  $b=100$ mm de l'axe de rotation propre.
Attention, on ne parle pas ici d'effet gyroscopique qui provient de la force globale de portance et de son point d'application ...

suivant: Exploitation monter: Analyse des efforts sur précédent: Remarques