suivant: Centre de poussée monter: Exploitation précédent: Remarques

Energie

On peut estimer [On ne prend en compte ici qu'une translation rectiligne et la seule vitesse de rotation propre du tripale !] l'energie cinétique (exprimée en Joule) du tripale avec :

 $$E_c = \frac 1 2 m V^2 + \frac 1 2 I \Omega^2$$

A l'instant initial cette énergie vaut :

 $$E_{c\>i} = \underbrace{\frac 1 2 m V_i^2}_{6.81 \mbox{ \tiny... ...rac 1 2 I \Omega_i^2}_{5.55 \mbox{ \tiny J}} = 12.36 \mbox{ J}$$

A l'instant final cette énergie vaut :

 $$E_{c\>f} = \underbrace{\frac 1 2 m V_f^2}_{3.75 \mbox{ \tiny... ...frac 1 2 I \Omega_f^2}_{2.74 \mbox{ \tiny J}} = 6.50 \mbox{ J}$$

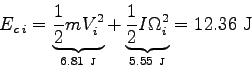
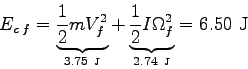
Soit une perte d'énergie de 5.86 J soit 47% de l'énergie initiale (45% de perte en translation et 50% en rotation). Cette énergie a été perdue par la force de trainée et par le couple de freinage et peut être calculée par les puissances perdues par ces actions.

La puissance perdue par la force de trainée est  ${\cal P}_1=-T V$ or $V$ dépend du temps ($T$ aussi mais on l'a considéré constant). L'énergie perdue est calculée par :

 $$E_1 = \int_{t_i=0}^{t_f=\Delta t} {\cal P}_1 \> \mbox{d}t = \dots \approx - \frac 1 2 T (V_f+V_i) \Delta t = - 3.06 \mbox{ J}$$

La puissance perdue par le couple de freinage est  ${\cal P}_2=-{\cal C} \Omega$ or $\Omega$ dépend du temps (${\cal C}$ aussi mais on l'a considéré constant). L'énergie perdue est calculée par :

 $$E_{c2} = \int_{t_i=0}^{t_f=\Delta t} {\cal P}_2 \> \mbox{d}t... ...c 1 2 {\cal C} (\Omega_f+\Omega_i) \Delta t = - 2.81 \mbox{ J}$$

L'énergie cinétique initiale (précédemment calculée) a été fournie par le lanceur en développant une certaine puissance ${\cal P}_L$ durant le laps de temps du lancer $\Delta t_L$. En considérant que ${\cal P}_L$ est constante durant tout le laps de temps du lancer on a :

 $$E_{c\>i} = {\cal P}_L \Delta t_L$$

En prenant une puissance de 200 W on obtient  $\Delta t_L = 0.0618$ s. 

En prenant  $\Delta t_L=0.05$ s $=\frac 1 {20}$ s, on obtient 247 W. 

Ces valeurs paraissent raisonnables mais sont peut être loin de la vérité ...

Ceci signifie qu'un lanceur développerait 247 W durant les 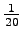$\frac 1 {20}$^ème de seconde d'un lancer pour amener ce tripale à une vitesse linéaire de $V=60$ km/h et une vitesse de rotation de $\Omega=25$ tr/s.

suivant: Centre de poussée monter: Exploitation précédent: Remarques