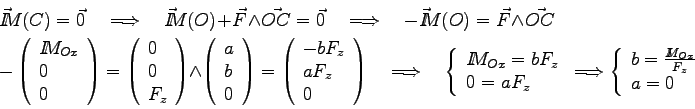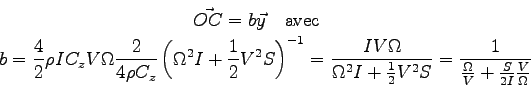suivant: Changement de base de
monter: Résumé
précédent: Résumé
Déterminons la position du centre de poussée  situé dans le plan du quadripale au même niveau que
situé dans le plan du quadripale au même niveau que  :
:
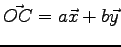 .
.
Le centre de poussée  (de la composante
(de la composante
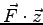 ) est positionné par :
) est positionné par :
C'est la même expression que la position moyenne sur le tripale.
Laurent Blanchard
2007-12-29
![]() situé dans le plan du quadripale au même niveau que
situé dans le plan du quadripale au même niveau que ![]() :
:
![]() .
.