suivant: Moments d'inertie et quadratique
monter: Section et moment quadratique
précédent: Pale rectangulaire
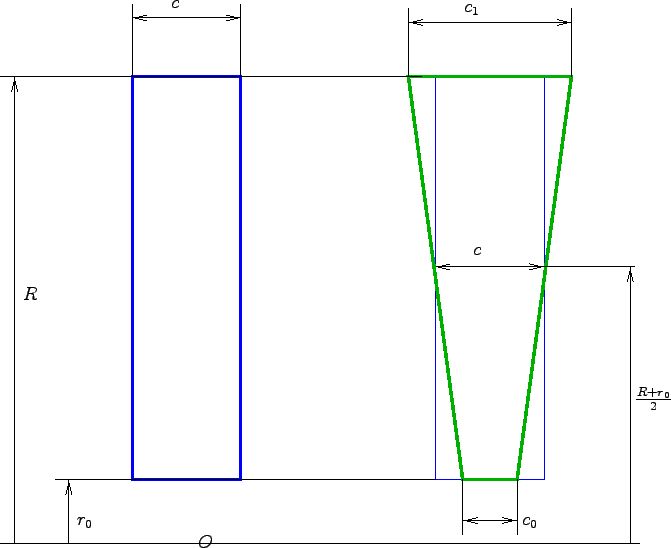
Cette expression étant compliquée, posons 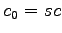 (
(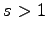 : pale moins large à l'extrémité,
: pale moins large à l'extrémité, 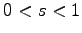 pale plus large à l'extrémité).
pale plus large à l'extrémité).
On retrouve bien le résultat d'une pale rectangulaire en prenant un cas particulier de pale trapézoïdale.
En comparant les pales rectangulaire et trapézoïdale qui ont même surface mais 2 inerties différentes 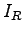 et
et 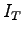 on a, lorsque
on a, lorsque 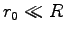 (pour simplifier la comparaison) :
(pour simplifier la comparaison) :
Et au vue de l'expression de  :
:
en comparant à 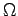 et
et 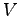 identiques on a :
identiques on a :
D'où l'intérêt
d'élargir la pale entre le centre du tripale et
l'extrémité de la pale pour augmenter l'effet
gyroscopique (attention à ce type de conclusion !).
Laurent Blanchard
2007-12-29

![\begin{displaymath}\displaylines{
\mbox{d}S = c(r) \> \mbox{d}r
\quad\mbox{ où...
...0^4 -2c_0Rr_0^3
+ 3cR^4
- c_0R^4 + c_0r_0^4
\right]
\cr
}\end{displaymath}](img123.png)
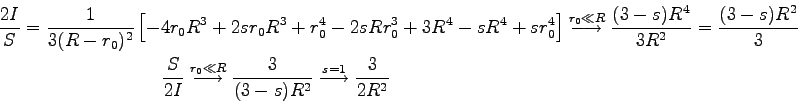
![]() et
et ![]() on a, lorsque
on a, lorsque ![]() (pour simplifier la comparaison) :
(pour simplifier la comparaison) :
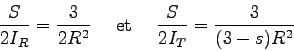
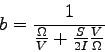
![]() et
et ![]() identiques on a :
identiques on a :