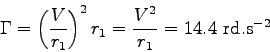suivant: Quadripale monter: Application numérique sur le précédent: Efforts aérodynamiques

Autres efforts

En prenant une masse 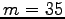$m=35$ g, le poids du boom est de l'ordre de 0.34 N

En considérant que la trajectoire du boom est un cercle de rayon 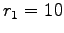$r_1=10$ m , il "tourne" à  une vitesse :

 $$\frac V {r_1}=1.2 \mbox{ rd.s$^{-1}$} (\approx 11.5) \mbox{ tr/mn}$$

ce qui fait un vol de 5.2 s pour ce tripale de 20 m de portée : ce qui est un peu important ! Le boom subit alors une accélération centrifuge :

 $$\Gamma = \left( \frac V {r_1} \right)^2 r_1 = \frac {V^2}{r_1} = 14.4 \mbox{ rd.s$^{-2}$}$$

et une force due aux effets centrifuges :

 $$m \Gamma = 0.5 \mbox{ N}$$

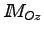De plus  $I \kern-4.5pt M_{Oz}$ freine la rotation 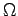$\Omega$. On peut évaluer la variation de vitesse de rotation par :

 $$\dot\Omega = \frac{I \kern-4.5pt M_{Oz}}{J} = - 43 \mbox{ rd.s$^{-2}$} = - 6.8 \mbox{ tr.s$^{-2}$}$$

soit une diminution de 35 tr.s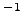$^{-1}$ au bout des 5.2 s de vol !!! ce qui ne va plus ! 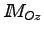 $I \kern-4.5pt M_{Oz}$ est donc plus faible !?